I had been engaged in an email exchange with a reader very recently about my soccer Pythagorean which required me to revisit the expression.  I came to look at the Pythagorean in a slightly different way, but one that improved my own understanding of it.  I’d like to share it and hopefully it will be meaningful to you.

When I wrote my last big post on the soccer Pythagorean, I said that Pythagoreans are nothing more than win/loss/draw probability calculations given the expected averages of goals scored and goals allowed.  The term “expected” is important — the means are adjusted by a translation parameter in the soccer Pythagorean (they’re also adjusted in the baseball Pythagorean that Steven Miller derived but not in Bill James’ original).  They are also joint probabilities in that we are considering the probability that team X has scored c goals and team Y has scored less than c goals in the same match.  (We use team X’s offensive and defensive goal averages to come up with both probabilities, and some sharp people will object that team Y has its own influence as well, but it’s an approximation that serves us well.)

What makes the soccer Pythagorean different from those for basketball, baseball, and American football is that we have to deal with drawn results, so we have to sum probabilities over the possible range of goals scored. Practically this means that for win probabilities we sum up to 10 and for draw probabilities we sum up to 6 (a 6-6 draw).  If you come across a league where a team has scored more than 10 goals in a match, just increase the range of summation.

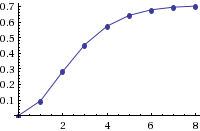
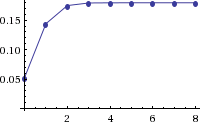
If you look at the partial sums of the Pythagorean, they look something like they do in the figures below.  Here they are for Manchester City’s final Pythagorean estimate in the 2011-12 Premier League season.

Cumulative Pythagorean win probability, Manchester City in EPL 2011-12 (FINAL)

Cumulative Pythagorean draw probability, Manchester City in EPL 2011-12 (FINAL)

Given City’s averages of 2.45 goals scored/match and 0.76 goals allowed/match, they would be expected to win 70.3% of their matches and draw 17.9%.

As you would expect, the cumulative draw probability flat-lines (hits its asymptote, to be way too technical) pretty quick.  Very few score draws beyond 3-3 were scored in the Premier League (there was one 4-4 between Swansea and Wolves).  It’s interesting to observe that scoring no goals gives City a 5% probability of a draw — zero probability for a win, of course.  The cumulative win probability maxes out around six or seven goals; this is the probability that team X will score c goals and team Y will score less than that.  The probability of the second event may be 1.0, but the probability of the first could be very small, which would result in a very small number.  So the soccer Pythagorean is computing the cumulative joint probability of a win and a draw.

Pythagoreans in general calculate cumulative joint probabilities, but in sports that don’t have draws many of the terms are cancelled out.  For sports that have lots of draws — like soccer — the Pythagorean doesn’t have that convenience.  But it all works the same.