I’m a naturally curious guy, and the other day my curiosity guided me to weather conditions at sporting events.  I was on a site called British Weather Services which is a group of private sector meteorologists who provide forecasts and consulting services for a variety of clients in the UK, sports bettors among them.  My eyes drew me to a remarkable blog post entitled, “COLD KILLS GOALS – THE STATS“.  Here’s the salient point of the article:

Bottom Line:  Cold or sub zero temps do not guarantee below 2.5 goals in any one match, but over a spread of matches the colder temperatures do help reduce the expected goal tallies and when the sub zero matches are clumped together (the 6) the goal tallies tend to shrink further.   Cold kills goals, FACT.

(Emphasis theirs.) I guess my hackles were raised by a statistical post that made such a strong statement on so little data (16 matches played on one day in the 2012-13 UEFA Europa League!!), but it did get me thinking: what is the effect of temperature on goal scoring in football?  And is the effect significant enough to matter?

To start to answer these questions, I took kickoff temperature and goal scoring data from matches in the 2011-12 Premier League, which incidentally is available from the beta version of the Soccermetrics API.  So a total of 380 observations are taken.  I consider the effect on goal scoring with the over/under metric, which is an informal standard to assessing whether a football match is high-scoring.  The dependent variable is \(P(O/U>2.5)\) or the proportion of matches in which the over/under is greater than 2.5 goals, which is arbitrary of course but also the standard number given by betting houses and just below the three-year Premier League average of 2.8 goals per game.

So what was the spread of temperature and total goals in Premier League matches in 2011-12?  Something like this:

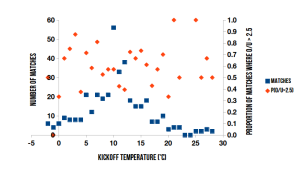
Variation of kickoff temperature and matches with over/under exceeding 2.5 goals, 2011-12 English Premier League.

The distribution of matches with temperature follows a normal distribution, as does the raw number of matches in which the O/U exceeds 2.5.  However, the proportion of matches that were high-scoring at each temperature reading don’t appear to follow any kind of discernible pattern.  It is accurate to say that there were fewer matches with more than two goals scored when the temperature dropped below 5 degrees Celsius.  But then again, there were fewer matches being played under 5 degrees Celsius — at least in England.

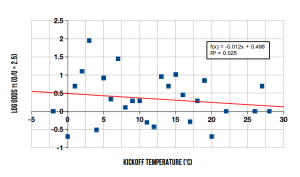
So how sensitive is O/U to temperature?  I perform a logistic regression analysis to examine that question.  It’s a very simple (crudely simple) regression:

\[
\log \frac{\pi}{1-\pi} = \beta_0 + \beta_1 x_1
\]

where \(\pi\) represents \(P(O/U > 2.5)\).  It’s a linear regression on the log odds of \(P(O/U > 2.5)\).  The resulting coefficients are \(\beta_0 = 0.498 \pm 0.018\) and \(\beta_1 = -0.012 \pm 0.002\).  For a single regressor it’s straightforward to display a graph, so here is one below.

Kickoff temperature regression on log odds of O/U>2.5, 2011-12 English Premier League season.

So for every degree Celsius increase in playing temperature, the estimated odds of \(P(O/U > 2.5)\) decrease by 1.2%.  Translated to probabilities, the difference in magnitudes at various temperature is not that great.  At zero degrees Celsius, the estimated \(P(O/U > 2.5)\) is 0.62, which of course means that \(P(O/U < 2.5)\) is 0.38.  At 10 degrees Celsius, it is 0.59.  Not a big difference.

There are so many caveats with this analysis to cover this post with yellow caution tape.  For starters, we are only considering one regressor: kickoff temperature.  Predominant weather condition might be another condition worth adding (zero Celsius and clear is a different environment from zero Celsius and snowing), but that would add a categorical variable that I didn’t want to deal with at the time.  There could be other meteorological variables that might be important — wind speed, humidity — but those aren’t always available readily.  (The J-League reports temperature and humidity in their match reports for reasons that aren’t clear to me.)

The most significant caveat is the need for more data beyond a single season.  I feel very uncomfortable making a strong conclusion on a season’s worth of data from a single domestic competition.  What should one think of a categorical statement made with data from one night of a continental club competition?