Knowing when the ball is out of play (“ball-out” events) in football is important in order to calculate effective playing time and the possession metrics of the two teams.  But what do you do when you don’t have ball-out data?  In this post I present a calibration tool to estimate match time lost due to ball-out events.

My motivation for the post comes from work on the Soccermetrics Connect API during the World Cup this summer.  One of the lessons I learned from the API (which really deserves a separate post of its own) is that no matter how hard one tries to standardize data processing and analysis code, there will always be peculiarities from a data supplier that will make that task extremely difficult.  In the case of Press Association’s MatchStory, which supplied the touch-by-touch data for the World Cup, there are no recorded events of the time and location of the ball going out of play.  MatchStory does record throw-ins, corner kicks, and goal kicks, which are the “restart events” from a ball going into touch or over the bye lines.

So why do I care about ball-out events?  Without them, it is difficult to calculate effective playing time or possession time in a match because it is impossible to know precisely when a spell of possession stops and the dead period of the ball out of play begins.  At the extremes, one could consider the possession as continuing to the throw-in, corner, or goal kick and ignore time lost due to the ball going out of play, which would overestimate possession time and underestimate effective time, or consider the touch event preceding the throw-in, corner, or goal kick as the start of the stoppage, which underestimates the possession time and overestimates the effective time.  As a compromise, one could employ something like a “90/10 rule” in which one assumes that in the time between the touch event preceding the restart event and the event itself, for the first 90% of the play the ball is in play and in the last 10% it is not.  But the assumption is kludgy and tricky to implement.  (I pulled a 90/10 figure out of the air; I have not tested that assumption with any data.)

Ball-out events are not trivial in a football match.  Consider that in a typical football match, 55-75 ball-out events occur, which translates to 10-20 minutes playing time lost.  It also means that effective time could be off by as much as 5-8 minutes.  Possession time — and ultimately match tempo — are even more difficult to estimate.

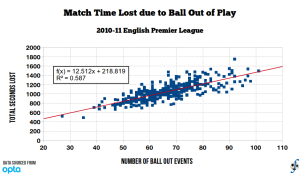
So MatchStory does not contain ball-out events, which is unfortunate but the reality that must be faced.  One remedy to this problem is to correlate the number of ball-out events to the amount of playing time lost, and use that figure to correct our original estimate of effective playing time.  Fortunately I do have an available dataset, thanks to Opta Sports.  This ball-out data is from the 2010-11 English Premier League, and we calculated time lost by implementing a state transition model of continuous play and stoppages in a football match.  A least-square fit between the number of ball-out events and the total seconds lost yields the relationship described in the figure below.

Match time lost due to ball-out events in 2011-12 English Premier League matches.

Obviously the regression constants have error terms associated with them, which are:

α₀ (constant) = 218.819 ± 36.624

α₁ = 12.512 ± 0.540

There appears to be a good relationship between the number of ball-out events and the total seconds lost, which isn’t too surprising.  It doesn’t tell us anything definitive about the quality of the fit, and I didn’t perform a goodness-of-fit test or a t-test on the regression constants.  But the magnitude of the standard errors gives me some confidence that those constants are significant from zero.

One defect of the linear regression is that it does not intersect at zero, which means that a match with zero ball-out events has non-zero time lost due to ball-out events.  This is nonsensical, of course, and one remedy is to use a power model regression, where

f(x) = ax^b

One can calculate the regression constants by transforming the data to a log-log scale, but I didn’t do that here.  I’ll present those calculations later.  In reality, I expect few matches to experience fewer than 20 events where the ball is out of play, unless the match is highly scripted.

The bottom line is that I have a calibration model that allows me to estimate how much time should be lost due to ball-out events.  It’s not perfect, and it could use more points, but it is a start.  Of course, I would rather not use this approach and know exactly when a ball has left the field of play.  But not all data providers have that capability.

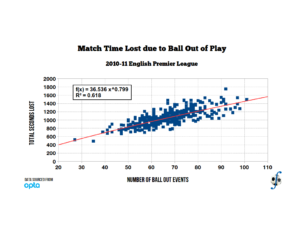
UPDATE: I carried out a power model regression and got these results for the model:

a = 36.525 ± 1.305

b = 0.7994 ± 0.064

The uncertainties represent the intervals of the regressors at a 95% confidence level.  The coefficient of determination R² is 0.618, which means that this model captures a little bit more of the variance than the linear model, but I don’t the difference is that great.  There is still a non-zero time lost if there are no ball-out events, but such an occurrence will never happen.

Power model regression of time lost due to ball out events, 2010-11 English Premier League.