Description

This publication presents a formulation of an extension to the Pythagorean expectation for association football and other sports in which a draw result is a nontrivial event. Instead of estimating win percentage as in baseball, the extended Pythagorean estimates points won per game.

We use a least-squares algorithm to fit offensive and defensive goal distributions to a three-parameter Weibull distribution, of which the parameter of interest is the Pythagorean exponent.

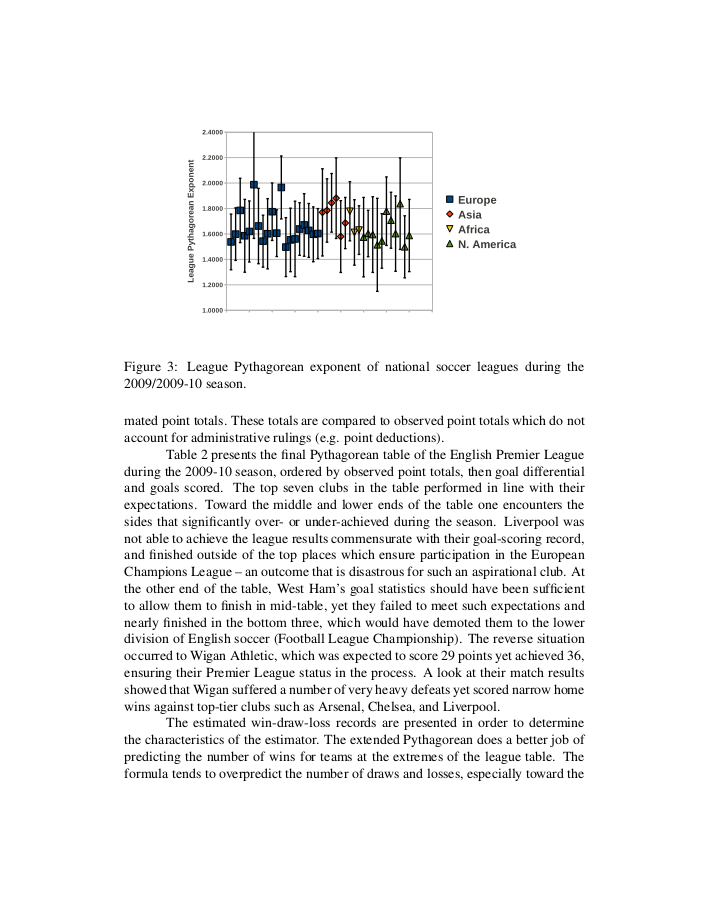
Further analysis reveals that the league Pythagorean exponent remains stable across multiple leagues in the same calendar year and within a single league over multiple seasons, which gives support to the notion of a “universal” Pythagorean exponent.

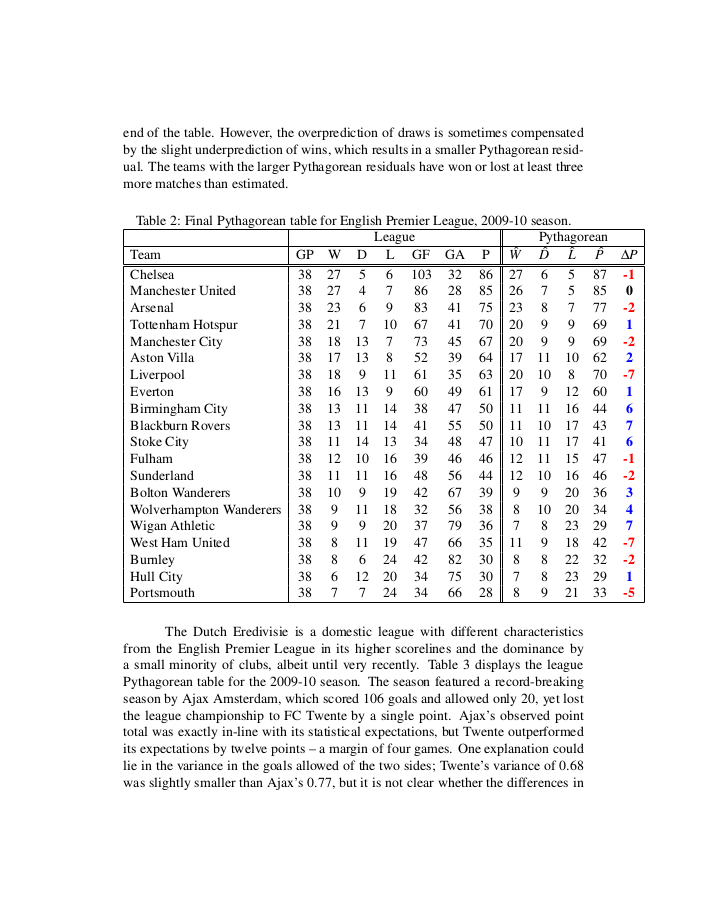
Application of the extended Pythagorean to results of domestic soccer leagues in Europe, Asia, and the Americas shows excellent agreement between goal statistics and league records for a majority of teams, and it indicates the teams that strongly overperform or underperform with respect to their expected performance.