Lionel Messi’s 21-match goalscoring streak this La Liga season is the longest seen in domestic football competitions in 75 years (16 matches by Teodor Peterek for Polish side Ruch Chorzów in 1937-38).  Whenever streaks in sport are discussed, it’s inevitable that someone — especially if that someone is American — will mention Joe DiMaggio’s 56-game hitting streak for the New York Yankees in 1941.  DiMaggio’s streak is considered one of those statistically improbable sporting records that may never be broken.  Does Messi’s streak belong in the same category?  Will we have to wait 75 years or more for a similar streak in a league competition? And perhaps most importantly, are both streaks really all that significant?

When I was preparing this piece, I did a literature search of the mathematics surrounding the DiMaggio streak, believing that there would be some analysis showing how exceptional it was.  That analysis does exist (here’s one example, and another by the wonderfully named Don Chance), but I found much more.  As a matter of fact, the streak continues to attract debate in sabermetric circles, and there is considerable disagreement over the significance of DiMaggio’s feat.  In 2008 Samuel Arbesman and Steven Strogatz published the results of a Monte Carlo simulation of Major League Baseball seasons between 1870 and 2005, in which they reported that a DiMaggio-like streak occurred 42% of the time.  The paper drew critiques and defenses in equal measure (cf. this defense of DiMaggio’s feat by Carl Bialik in the Wall Street Journal, with further comment by Phil Birnbaum, and a counterargument by Leonard Mlodinov in the WSJ the following year).

Even though it’s quite clear from the DiMaggio debate that any argument about Messi’s record won’t be settled by this humble post, we can nevertheless use the statistical analysis as a starting point for assessing the scoring streak.  There are three questions to be answered:

• How likely is a 21-match goalscoring streak in football?
• How likely was Lionel Messi to score in 21 consecutive matches?
• How likely is an average player to match Messi’s feat?

The first question is relatively easy to answer but there are a couple of controversial assumptions.  The other two are much more difficult to answer for a football competition and we’ll never reach an exact figure.  I’ll answer the first question in this post.

Let’s assume that the probability of scoring a goal in a match is γ, and we’ll further assume that the shot conversion rate is a good estimator of this probability.  (That’s the first controversial assumption as that rate is the result of limited samples from the true probability distribution, but let’s live with it.) The probability of not scoring a goal is (1-γ). If a player has α attempts at goal in a match, the probability of no goals in a match (assuming independent events) is:

Thus, the probability of a player scoring at least one goal in a match is:

Now how do we calculate the probability of a N-match scoring streak (we’ll call it κ)?  And here we see the second controversial assumption. We could assume that our player will have an average number of scoring chances in a match:

But that assumption fails to account for the variance in opposing defenses, so we can rewrite the expression as a chain of probabilities for individual matches multiplied together.  In other words:

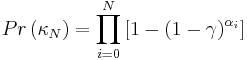
So what are the odds against such a streak occurring?  I’ll make some rough assumptions.  First, assume that the average player takes about 1.2 shots per match and converts on 10% of those chances. (Strikers may be a little more, defenders a little less.)  Next, let’s assume that Lionel Messi takes about 3.0 4.3 shots per match and converts on 30% 25% of those chances, which seems reasonable given his performance the last five seasons.  Just for kicks, let’s throw in Cristiano Ronaldo who has taken about 3.0 6.2 shots per match and converted on 17% 15% of them over the last five seasons.

(Thanks to Simon Gleave at Infostrada Sports for providing me with more correct shot data on the two players.)

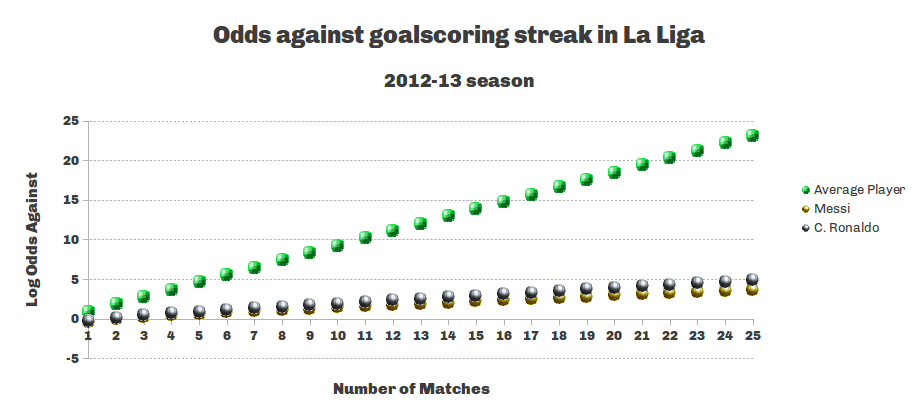
I’m going to use the third equation to calculate the probability of an N-match goalscoring streak.  Because that number tends to be very small, let’s express that probability in terms of log odds.  Plots for all three players are described in the figure below.

For the average player, the odds against achieving a 21-match goalscoring streak are about 10^21 to one – a sextillion to one!  Having more attempts at goal in a match reduces the odds against significantly, and increasing the shot conversion rate reduces them further.  The odds against Cristiano Ronaldo having a 21-match streak are about 54 million 14,000 to one.

The odds against Messi achieving such a streak given his average performance over the last five seasons? A little over 1300 to one.  It’s a remote chance, but imaginable enough to place a bet on it.  (The odds against a 11-match streak for Messi — which Gabriel Batistuta accomplished for Fiorentina in 1994-95 — are only 30 to one.)  I’d love to see what prices the betting houses in London were placing on a Messi streak.  So it appears the combination of high scoring chances and clinical finishing create the conditions for these long goalscoring streaks, and that combination is very rare among professional footballers.

And how do the odds against Messi’s streak compare with the odds against DiMaggio’s streak?  If you make the same crude assumptions — batting average .357 in 1941 with four at-bats per game — the odds against a 56-game streak are a little over 36,000 to one.

As I said, the calculation of both streaks are flawed — a more precise analysis would shorten the odds in the case of DiMaggio’s streak and perhaps lengthen them in the case of Messi’s.  We’re still assuming that these players will receive the same number of chances in each game, which is a very optimistic assumption.  Nevertheless it does appear that Messi’s achievement is more likely yet more exceptional than the baseball analogue.  In some future posts I’ll present some analysis to further test those observations.

CORRECTIONS: I’ve corrected some of the numbers and the plot to reflect more accurate assumptions of the goalscoring statistics. Thanks to Simon and Ted Knutson (@mixedknuts) for pointing them out.